固有値や固有ベクトルの計算では、変数(代数)を含んだ状態で計算したくなることがあります。Pythonを用いて変数を用いた固有値、固有ベクトルの計算するコードを作成しました。
計算に用いる行列式
以下のような2×2の\(\tilde{\varepsilon}\)の行列に対して固有値\(\lambda\)と固有ベクトル\(\left(
\begin{array}{cc}
E_{x} \\
E_{y}
\end{array}
\right)\)を求める場合を例に説明します。
$$
\left(
\begin{array}{cc}
\varepsilon_{xx} & \varepsilon_{xy} \\
-\varepsilon_{xy} & \varepsilon_{xx}
\end{array}
\right)\left(
\begin{array}{cc}
E_{x} \\
E_{y}
\end{array}
\right)=\lambda \left(
\begin{array}{cc}
E_{x} \\
E_{y}
\end{array}
\right)
$$
コード概要
Sympyライブラリを用いて固有値と固有ベクトルの計算を行いました。変数をSymbolとして設定すれば、数値の場合と同様に簡単に固有値・固有ベクトルを求めることができます。
数値の場合
$$
\tilde{\varepsilon}=\left(
\begin{array}{cc}
0 &2 \\
1 & 4
\end{array}
\right)$$
のとき、以下のように固有値と固有ベクトルが求まります。例えば固有値は\(2\pm\sqrt{6}\)となります。
from sympy import *
epsilon = Matrix([[0, 2], [1, 4]])
print(list(epsilon.eigenvals().keys()))#固有値を求める
#[2 - sqrt(6), 2 + sqrt(6)]
print([list(tup[2][0]) for tup in epsilon.eigenvects()] ) #固有ベクトルを求める
#[[-sqrt(6) - 2, 1], [-2 + sqrt(6), 1]]変数を用いた場合
\(\tilde{\varepsilon}\)の変数をそのまま用いる場合、最初に変数を宣言します。
e_xx,e_xy = symbols("e_xx e_xy ")
epsilon=Matrix([[e_xx, e_xy],
[-e_xy, e_xx]])
print(list(epsilon.eigenvals().keys()))#固有値を求める
#[e_xx - I*e_xy, e_xx + I*e_xy]
print([list(simplify(tup[2][0])) for tup in epsilon.eigenvects()] ) #固有ベクトルを求める。simplifyで数式整理。
#[[I, 1], [-I, 1]]変数を用いるメリット
固有値や固有ベクトルが変数を用いて求まっているので、変数の値をforループで変化させたときの挙動が簡単に調べられます。
今回用いた例では固有値の実部が\(\varepsilon_{xx} \)、虚部が\(\pm\varepsilon_{xy} \)と単純ですが、実際には変数の数がもっと増えて直感的に分かりづらくなってきます。変数を用いてシンプルにまとめることができると便利だと思います。
Copyright © 2001-2020 Python Software Foundation; All Rights Reserved
Copyright © 2022 Released under the BSD License https://opensource.org/licenses/BSD-3-Clause

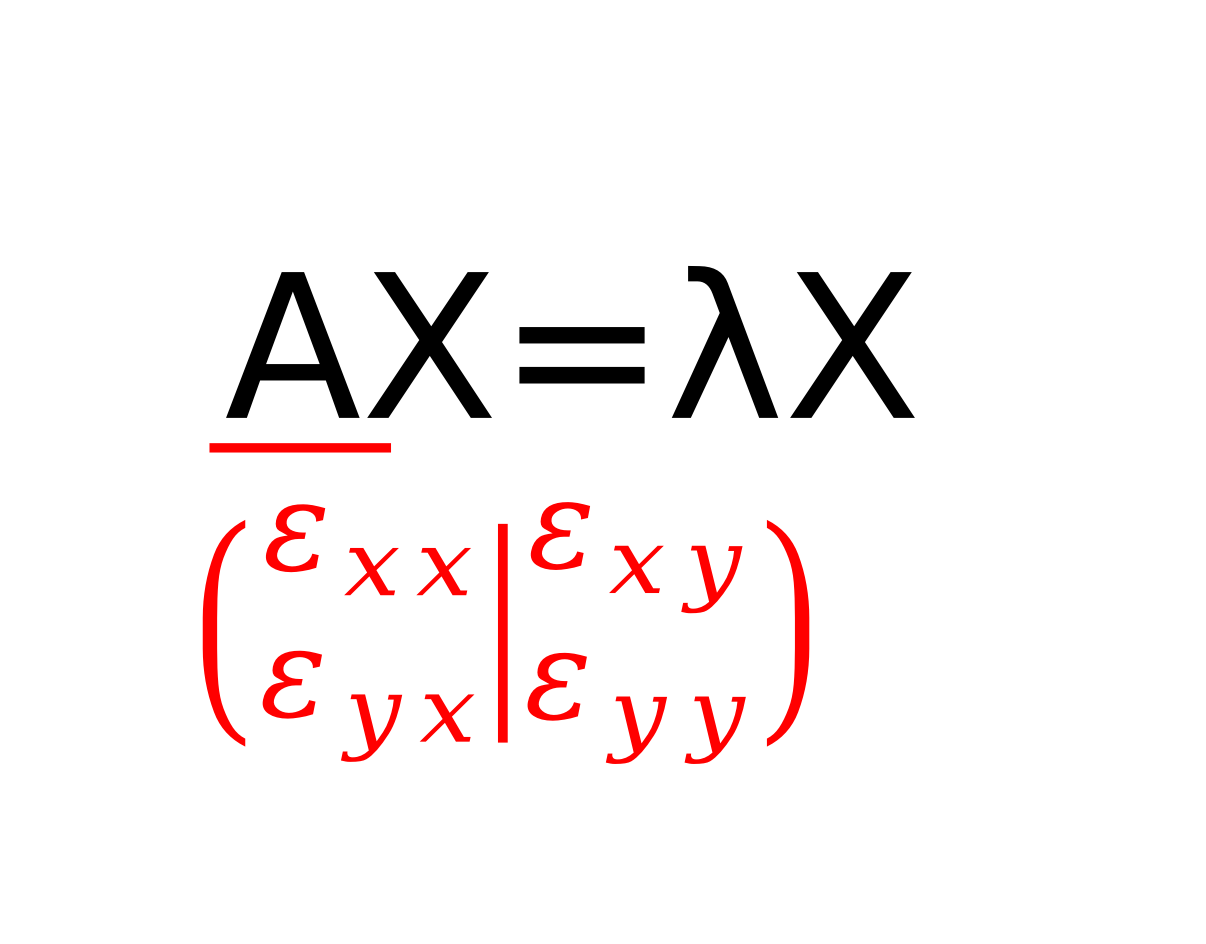

コメント