設計値と実験値の間で一定量のずれが生じ、それを補正しなければならないときがあります。2次元極座標補正のためのパラメータを勾配降下法で求めるプログラムを作成しました。
テストデータ作成
#ライブラリインポート
import matplotlib.pyplot as plt
from sklearn.datasets import make_gaussian_quantiles#https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_gaussian_quantiles.html
import numpy as np
from mpl_toolkits.axes_grid1 import make_axes_locatable
from scipy.stats import norm
from scipy.optimize import curve_fit
from mpl_toolkits.mplot3d import Axes3D
#Copyright © 2001-2020 Python Software Foundation; All Rights Reserved
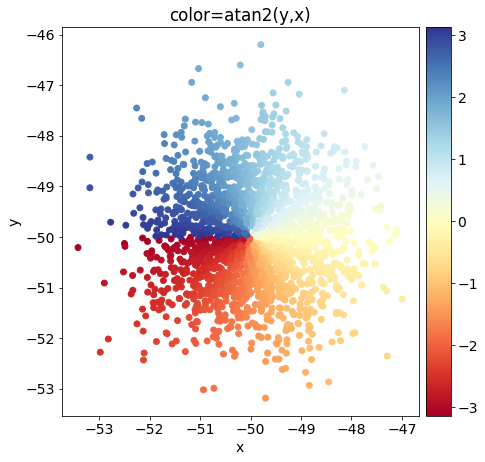
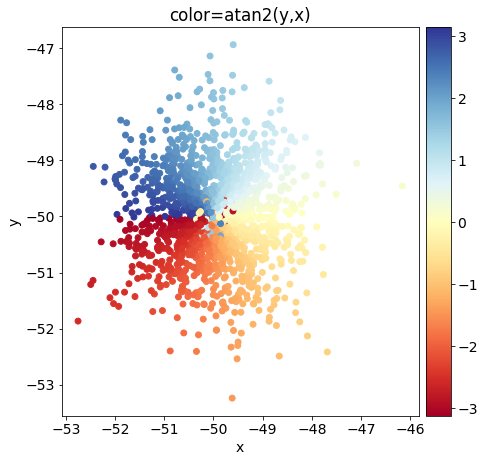
#Copyright © 2022 Released under the BSD License https://opensource.org/licenses/BSD-3-Clause直交座標系なら微分値の計算が簡単ですが、回転ずれなどが生じている可能性を考慮すると極座標系で考える必要があります。今回は以前紹介したカラープロットをもとに、位置(aveX,aveY)を中心としたガウス分布を基準データ0として用います。
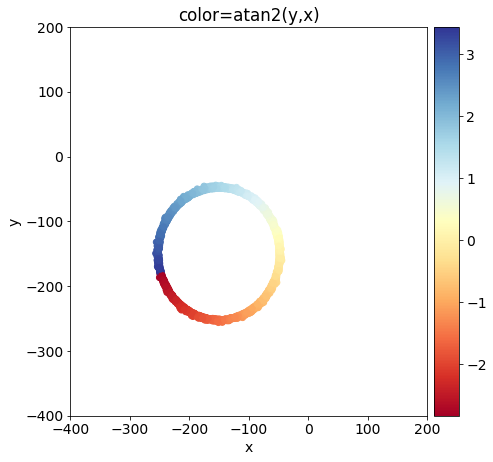
ガウス分布にRθ座標系での位置ずれ(ΔR、Δθ)=(100,0.3)、さらにXY座標系でのずれ(ΔX、ΔY)=(-100,-100)を加えたデータ1を作成しました。
位置ずれの大きさ評価方法
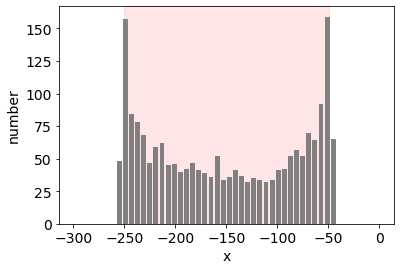
データ1のガウス分布のサイズを95パーセンタイルとして導出しました。なお、95%信頼区間が用いたデータから真の値(母集団)が95%の確率で見込まれる領域を示すのに対し、95パーセンタイルは単に用いたデータの下位95%の値の領域を示します(1、2、・・・100の100個の数字がある場合95パーセンタイルは1〜95の領域)。上位5%を外れ値とみなすことになります。
今回用意したデータ1では95パーセンタイル区間は[-250.67168711 -48.80599888]の領域となります。サイズは200程度となります(半径R〜100のため)。
ソースコード
#n_samples
data_list,label = make_gaussian_quantiles(n_samples=2000)
cm = plt.cm.get_cmap('RdYlBu')
#位置ずれ前の座標設定
aveX=-50 #X方向の平均値
aveY=-50 #Y方向の平均値
X0=data_list[:,0]+aveX #位置ずれ前のX座標
Y0=data_list[:,1]+aveY #位置ずれ前のY座標
#X軸からの角度theta導出
theta0=[]
for k in range(len(X0)):
theta= np.arctan2(Y0[k]-aveY, X0[k]-aveX)
theta0.append(theta)
theta0=np.array(theta0)#位置ずれ前のθ座標
R0=np.sqrt((X0-aveX)**2+(Y0-aveY)**2)#位置ずれ前の半径R
#位置ずれの大きさ設定
deltaR=100 #R方向の位置ずれ
deltatheta=0.3 #θ方向の位置ずれ
deltaX=-100 #X方向の位置ずれ
deltaY=-100 #Y方向の位置ずれ
#位置ずれ後の座標設定
R1=deltaR+R0
theta1=theta0+deltatheta
X1=X0+R1*np.cos(theta1)+deltaX
Y1=Y0+R1*np.sin(theta1)+deltaY
#位置ずれ前のカラープロット
fig0 = plt.figure(figsize=(6,6))
ax0 = fig0.add_axes((0.1, 0.1, 0.9, 0.9))
ax0.set_title("color=atan2(y,x)")
#ax.grid(which="both")#グリッド線を追加
ax0.set_xlabel("x")
ax0.set_ylabel("y")
#x_list,y_listの各座標における出力(z_list)をカラープロット
maingraph0=ax0.scatter(X0, Y0, c=theta0, vmin=min(theta0), vmax=max(theta0), s=35, cmap=cm)#z_listの最小値と最大値をカラースケールの最大値、最小値として用いる。
#カラーバーを追加
divider0 = make_axes_locatable(ax0) #グラフaxの外枠に仕切り(AxesDivider)を作成
color_ax0 = divider0.append_axes("right", size="7%", pad="2%") #append_axesで新しいaxesを作成
colorbar0=fig0.colorbar(maingraph0, cax=color_ax0 ) #新しく作成したaxesであるcolor_axを渡す。
plt.show()
#位置ずれ後のカラープロット
fig1 = plt.figure(figsize=(6,6))
ax1 = fig1.add_axes((0.1, 0.1, 0.9, 0.9))
ax1.set_title("color=atan2(y,x)")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_xlim(-400,200)#([min(X1),max(X1)])
ax1.set_ylim(-400,200)#([min(Y1),max(Y1)])
#x_list,y_listの各座標における出力(z_list)をカラープロット
maingraph1=ax1.scatter(X1, Y1, c=theta1, vmin=min(theta1), vmax=max(theta1), s=35, cmap=cm)#z_listの最小値と最大値をカラースケールの最大値、最小値として用いる。
#カラーバーを追加
divider1 = make_axes_locatable(ax1) #グラフaxの外枠に仕切り(AxesDivider)を作成
color_ax1 = divider1.append_axes("right", size="7%", pad="2%") #append_axesで新しいaxesを作成
colorbar1=fig1.colorbar(maingraph1, cax=color_ax1 ) #新しく作成したaxesであるcolor_axを渡す。
plt.show()
#位置ずれ後のヒストグラム
sample_1 = X1#norm.rvs(loc=100,scale=5,size=1000)
#print(sample_1)
num_bin=50
range_min=-300
range_max=0
hist_1, bins = np.histogram(sample_1, num_bin, range=(range_min,range_max))
bins = bins[:-1]
def extremities(array, pct):
# assert 50 <= pct <= 100
return np.percentile(array, [(100 -pct)/2, pct+(100 -pct)/2])#正負のデータを含む場合は大きさ順で2.5%~97.5%の範囲
arr= sample_1
pct_range=extremities(arr, 95)
print(pct_range)
print(pct_range.shape)
fig, ax = plt.subplots()
plt.axvspan(pct_range[0],pct_range[1], alpha=0.1, color="red")
plt.hist(sample_1,bins=num_bin,range=(range_min,range_max),rwidth=0.8, color="gray")
ax.set_xlabel('x')
ax.set_ylabel('number')
plt.show()
#Copyright © 2001-2020 Python Software Foundation; All Rights Reserved位置ずれの大きさ導出プログラム
位置ずれ補正の概要
座標補正の基本はパラメータが最適値のときに最小となる関数z(コスト関数)を設定することです。値を求めたいパラメータx,yの関数としてz=z(x,y)と表します。勾配降下法とは、zのx,y方向の勾配(偏微分)が0になる方向にパラメータ(x,y)を変化させていく手法で、放物線のように最小値・最大値が明らかな場合に適しています。
位置ずれがあると、設計値と実際の座標x,yの間の距離が有限となります。つまり、設計値(X0,Y0)と、今回対象とする座標(X1,Y1)があったとき例えば両者の距離の2乗をz=(X1-X0)2+(Y1-Y0)2と定義します。これは例えばX1に着目すると2次関数(放物線)なので、zの偏微分dz/dX1が0となる方向にX1を近づけていけば良いことになります。
極座標系(R1,theta1)は直交座標系(X1,Y1)に変換可能なので、上記と同様に考えることができます。ただし距離の2乗としてコスト関数を定義すると、R1が先に収束してしまうとtheta1は収束せずに発散してしまいます(例えばtheta1がどんな値をとろうとも、原点と座標(X1,Y1)の間の距離はR1で一定です。つまりtheta1は任意の値を取りえます。)今回は、距離の2乗に(theta1-theta0)2を足し合わせることで、角度を収束させました。
ソースコード
#位置ずれ補正をする座標リスト
x=X1
y=Y1
theta=theta1
R=R1
#基準位置の座標
#今回は最初に定義した中心(aveX,aveY)のガウス分布を基準座標とする。
aveX=-50 #X方向の平均値
aveY=-50 #Y方向の平均値
X0=data_list[:,0]+aveX #位置ずれ前のX座標
Y0=data_list[:,1]+aveY #位置ずれ前のY座標
theta0=[]
for k in range(len(X0)):
theta= np.arctan2(Y0[k]-aveY, X0[k]-aveX)
theta0.append(theta)
theta0=np.array(theta0)#位置ずれ前のθ座標
R0=np.sqrt((X0-aveX)**2+(Y0-aveY)**2)#位置ずれ前の半径R
#コスト関数zを定義
def f(deltaR,deltatheta):
hoseiR=R1-deltaR
hoseitheta=theta1-deltatheta
hoseiX=hoseiR*np.cos(hoseitheta)
hoseiY=hoseiR*np.sin(hoseitheta)
z=np.mean(1/2*((hoseiX-X0)**2+(hoseiY-Y0)**2)+(hoseitheta-theta0)**2)#(hoseitheta-theta0)**2を加えて角度補正をする
return z
# コスト関数の微分
def df(deltaR,deltatheta):
hoseiR=R1-deltaR
hoseitheta=theta1-deltatheta
hoseiX=hoseiR*np.cos(hoseitheta)
hoseiY=hoseiR*np.sin(hoseitheta)
dzddeltaR = np.mean((hoseiX-X0)*(-np.cos(hoseitheta))\
+(hoseiY-Y0)*(-np.sin(hoseitheta)))/(len(x))
dzddeltatheta = np.mean((np.dot((hoseiR*np.sin(hoseitheta)).T,(hoseiX-X0)) + np.dot((hoseiX-X0).T,(hoseiR*np.sin(hoseitheta)))\
+np.dot((-hoseiR*np.cos(hoseitheta)).T,(hoseiY-Y0))+np.dot((hoseiY-Y0).T,(-hoseiR*np.cos(hoseitheta))+2*(hoseitheta-theta0)*(-1)))/(1000000*len(x)))
dz = np.array([dzddeltaR, dzddeltatheta])
return dz
# 勾配降下法に必要なパラメータ
eta = 100 # 学習率
max_iteration = 1000 # 最大反復回数
deltaR0 = 0 # 初期値ΔR0
deltatheta0 = 0 # 初期値Δtheta0
deltaR_pred = [deltaR0] # ΔRの推移リスト(初期値ΔR0)
deltatheta_pred = [deltatheta0] # 描画用Δthata軌跡リスト(初期値Δtheta0)
train_loss_list=[]
# 勾配降下法:設定した最大反復回数まで計算
for i in range(max_iteration):
deltaR0,deltatheta0= np.array([deltaR0, deltatheta0]) - eta * df(deltaR0, deltatheta0)
loss=f(deltaR0,deltatheta0)
train_loss_list.append(loss)
deltaR_pred.append(deltaR0) # ΔRの軌跡をリストに追加
deltatheta_pred.append(deltatheta0) # Δthetaの軌跡をリストに追加
deltaR_pred = np.array(deltaR_pred)
deltatheta_pred = np.array(deltatheta_pred)
z_pred = []
for i in range(len(deltaR_pred)):
z_pred.append(f(deltaR_pred[i],deltatheta_pred[i])) # 軌跡のz値を計算
z_pred= np.array(z_pred)
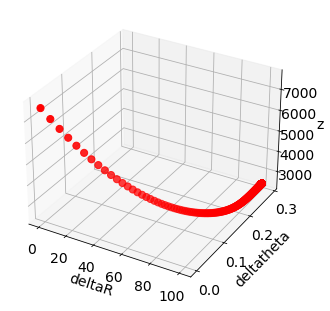
# 収束までのパラメータとコスト関数zの値の推移----------------------------------------------------------------
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'
# グラフの入れ物を用意
fig = plt.figure()
ax1 = Axes3D(fig)
# データプロットする。
ax1.set_xlabel('deltaR')
ax1.set_ylabel('deltatheta')
ax1.set_zlabel('z')
ax1.scatter3D(deltaR_pred, deltatheta_pred, z_pred, label='gd', color='red', s=50)
# グラフを表示する。
plt.show()
plt.close()
# ---------------------------------------------------------------------------------
#補正後の各座標
theta2=theta1-deltatheta_pred[-1]
R2=R1-deltaR_pred[-1]
X2=R2*np.cos(theta2)+aveX
Y2=R2*np.sin(theta2)+aveY
#位置ずれ補正後のカラープロット
fig2 = plt.figure(figsize=(6,6))
ax2 = fig2.add_axes((0.1, 0.1, 0.9, 0.9))
ax2.set_title("color=atan2(y,x)")
#ax.grid(which="both")#グリッド線を追加
ax2.set_xlabel("xaxis_title")
ax2.set_ylabel("yaxis_title")
#ax2.set_xlim(-400,200)#([min(X1),max(X1)])
#ax2.set_ylim(-400,200)#([min(Y1),max(Y1)])
#x_list,y_listの各座標における出力(z_list)をカラープロット
maingraph2=ax2.scatter(X2, Y2, c=theta2, vmin=min(theta2), vmax=max(theta2), s=35, cmap=cm)#z_listの最小値と最大値をカラースケールの最大値、最小値として用いる。
#カラーバーを追加
divider2 = make_axes_locatable(ax2) #グラフaxの外枠に仕切り(AxesDivider)を作成
color_ax2 = divider2.append_axes("right", size="7%", pad="2%") #append_axesで新しいaxesを作成
colorbar2=fig.colorbar(maingraph2, cax=color_ax2 ) #新しく作成したaxesであるcolor_axを渡す。
plt.show()
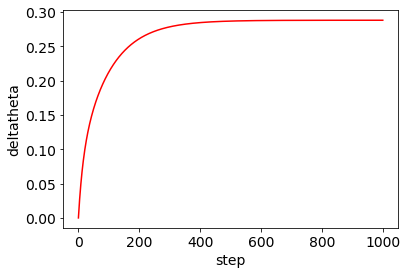
#Copyright © 2001-2020 Python Software Foundation; All Rights ReservedΔR,Δθの大きさの変化も以下のコードでチェックできます。
#ΔR,Δθの変化の履歴を見る
plt.plot(deltaR_pred,c='r',label='R')
plt.plot(deltatheta_pred,c='r',label='θ')
#Copyright © 2001-2020 Python Software Foundation; All Rights Reserved
位置ずれ補正の結果
今回の位置ずれ補正後の分布は以下のようになっており、もとのガウス分布が再現されていることがわかります。位置ずれの大きさが実験のたびに毎回似たような値を取る場合など、あらかじめ補正パラメータを導出しておけば毎回自動的に座標補正が可能です。
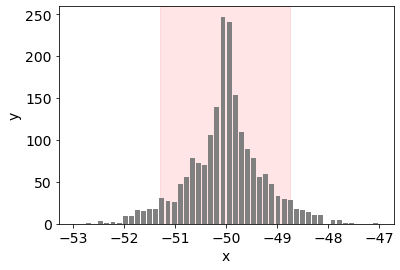
先ほど95パーセンタイルを導出したコードでX1(補正前)をX2と変えると以下のようなヒストグラム(今回は基準データに戻ったもの)となり、ガウス分布のサイズは3程度に補正されました。得られた補正パラメータ(今回はΔR,Δθ)が装置特有のものである場合、これを今後の測定での補正パラメータとして用いることができます。
まとめ
勾配降下法を用いて極座標系での位置ずれ補正とその分布のサイズ評価の方法をまとめました。他の手法や上手く収束させる方法などについて今後さらに検討してみたいと思います。


コメント