ファラデー効果で生じる偏光回転をPythonで再現してみました。光の性質として偏光がどれほど重要な意味を持つのかも伝えられたら良いと考えています。
偏光とは
光は電磁波の一種で、交流の電場・磁場成分を持ちます。身近な例だと、電池が直流電流を流そうとする力が電場です。太陽などから生じる自然光は電場の方向が色々な方向を向いており、偏りが無い(無偏光)状態です。無偏光状態の光は様々な偏光の光が互いに打ち消し合ってしまうため、遠くまで届きません(蛍光灯は部屋の中を照らす程度)。レーザー光は偏光した状態であり、壁などにぶつからなければそれよりもずっと遠くまで届きます(車間距離や星までの距離計測でも用いられています)。
偏光方向によって反射の仕方が異なる
偏光方向が違うと、物体に光が入射したときの反射率や透過率が変わります。この違いは偏光方向が物体への入射面内方向か面外方向かという違いから生じます。
入射面とP・S偏光
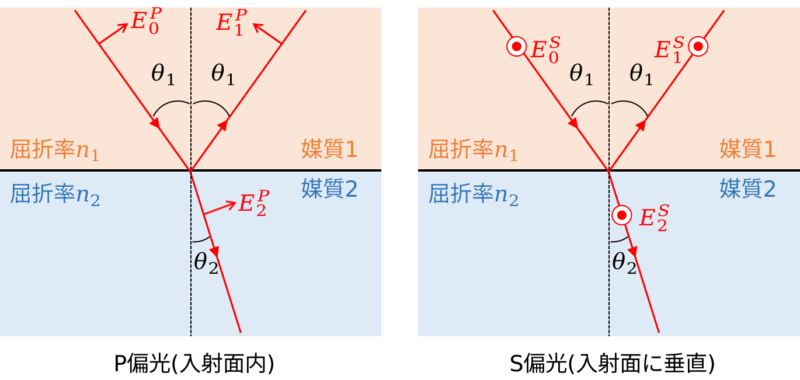
入射面とは、入射光の波数ベクトル(進む向き)と2つの媒質の界面の法線ベクトル(下図黒点線)を含む面のことです。P偏光は入射面に含まれる成分で、S偏光は入射面に垂直方向の成分(下図では画面手前方向)です。
2つの媒質界面内では電場は媒質1、2の間で連続的につながる、という条件によって偏光ごとの反射率、透過率を求めることができます。計算過程を知りたい方は『光と磁気』(朝倉書店、佐藤勝昭著)の3.5節をご参照ください(手計算で反射率・透過率係数導出を追うことができます)。この本を始め、佐藤勝昭先生の書かれた資料はどれも詳細且つ分かりやすいので、私も大学時代この本にとてもお世話になりました。
偏光で異なる反射率
反射・透過係数は入射角\(\theta_1\)、屈折角\(\theta_2\)、媒質1、2の屈折率\(n_1\)、\(n_2\)を用いてP、S偏光それぞれについて求まります。なお、屈折角\(\theta_2\)は入射角と各媒質の屈折率から求まるので、実質3変数(\(\theta_1\)、\(n_1\)、\(n_2\))となります。
媒質1から媒質2へ入射する際の反射係数\(r_{12}\)・透過係数\(t_{12}\)(ともに電場の大きさの比)は以下になります(S、P偏光を添字S、Pで区別)。
$$r_{12}^{S}=\frac{n_1cos\theta_1-n_2cos\theta_2}{n_1cos\theta_1+n_2cos\theta_2}$$
$$t_{12}^{S}=\frac{2n_1cos\theta_1}{n_1cos\theta_1+n_2cos\theta_2}$$
$$r_{12}^{P}=\frac{n_2cos\theta_1-n_1cos\theta_2}{n_2cos\theta_1+n_1cos\theta_2}$$
$$t_{12}^{P}=\frac{2n_1cos\theta_1}{n_2cos\theta_1+n_1cos\theta_2}$$
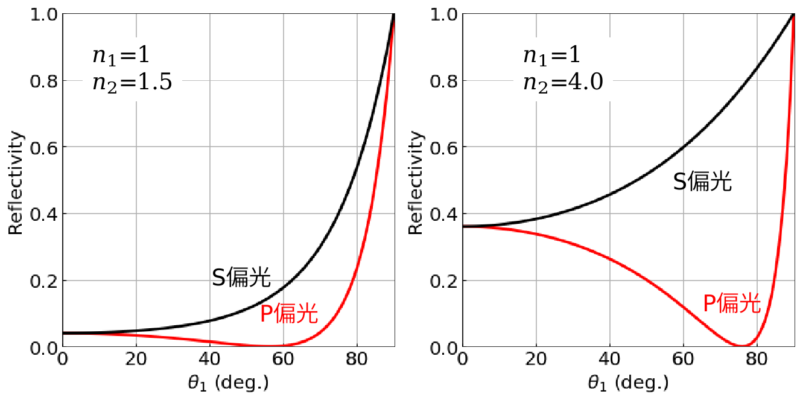
反射率R(入射光強度に対する反射光強度の比)を偏光ごとにプロットしたものが以下になります。屈折率の値は用いる光の波長や媒質によって異なります。屈折率\(n_1=1\)は空気、屈折率\(n_2=1.5\)は石英ガラス(SiO2)、屈折率(n2=4.0)はシリコン(Si)に対する可視光の屈折率を想定しています。
P偏光の反射率が0%(透過率が100%)になる角度(ブリュースター角)が存在しています(\(n_1=1、n_2=1.5\)のとき\(\theta_1\sim60\)度)。偏光によって反射率に大きな違いが生じます。上記グラフをプロットするのに用いたソースコードは以下です。
import scipy as sp
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy import pi,sin,cos,tan,arcsin,linspace
from matplotlib.pyplot import plot,show,xlabel,ylabel,title,legend,grid,axis,tight_layout
n1=1 #媒質1の屈折率
n2=1.5 #媒質2の屈折率
t1_deg=linspace(0,90,91)#入射角t1(deg)
t1=t1_deg/180*pi#入射角t1
t2=arcsin((n1/n2)*sin(t1))#屈折角t2
tp=2*n1*cos(t1)/(n2*cos(t1)+n1*cos(t2))#P偏光透過係数
rp=(n2*cos(t1)-n1*cos(t2))/(n2*cos(t1)+n1*cos(t2))#P偏光反射係数
ts=2*n1*cos(t1)/(n1*cos(t1)+n2*cos(t2))#S偏光透過係数
rs=(n1*cos(t1)-n2*cos(t2))/(n1*cos(t1)+n2*cos(t2))#S偏光反射係数
Rp=rp**2#P偏光反射率
Rs=rs**2#S偏光反射率
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.figure(figsize=(6,6))
plot(t1Deg,Rp,label=r"$r_{12}^{\rm{p}}$",linewidth=3.0,color='red')
plot(t1Deg,Rs,label=r"$r_{12}^{\rm{s}}$",linewidth=3.0,color='black')
xlabel(r"$\theta_1$ (deg.)",fontsize=20)
ylabel("Reflectivity",fontsize=20)
grid(True)
axis([0.0,90,0,1])
plt.tick_params(labelsize=20)
tight_layout()
show()ファラデー効果
ファラデー効果とは
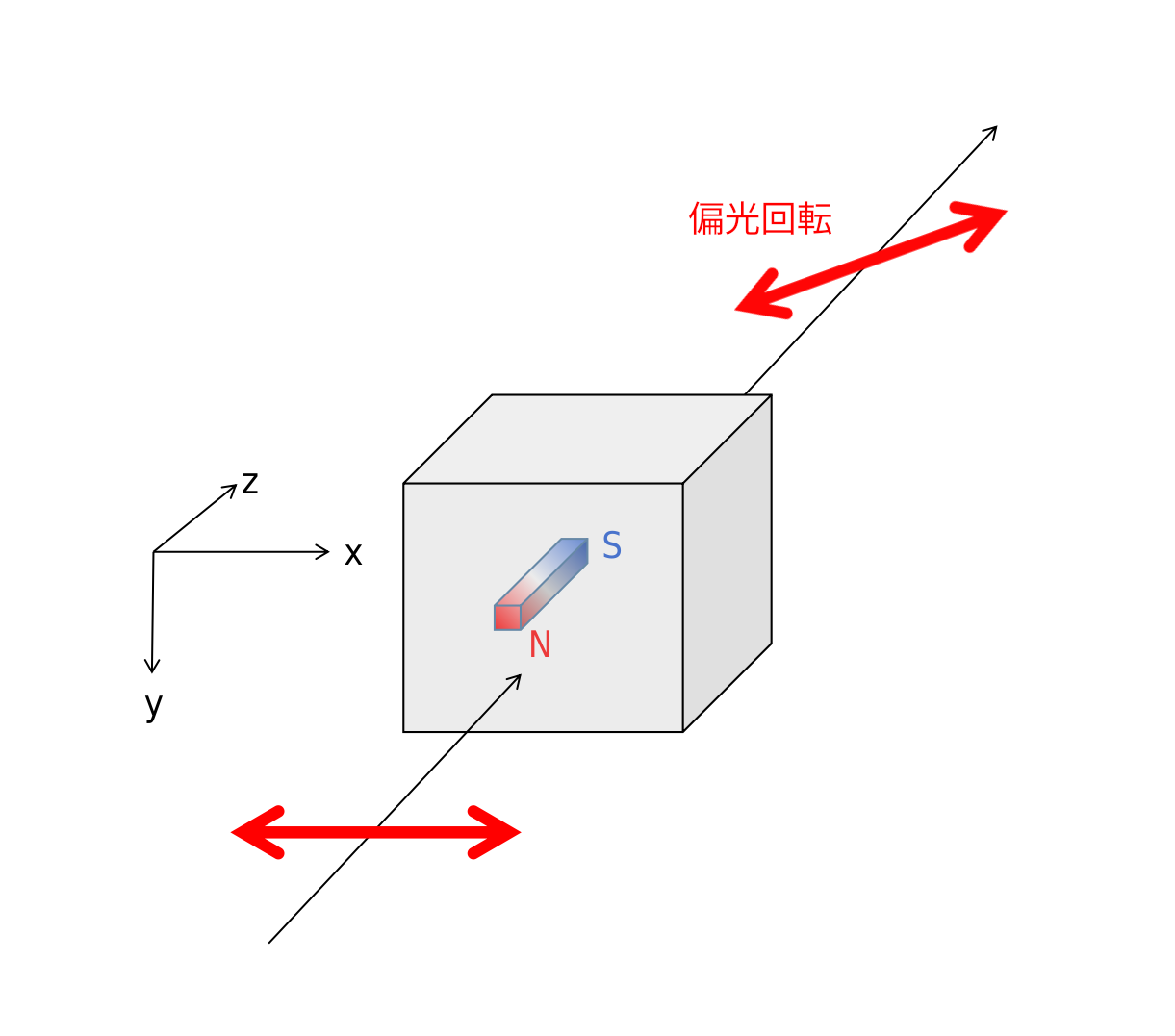
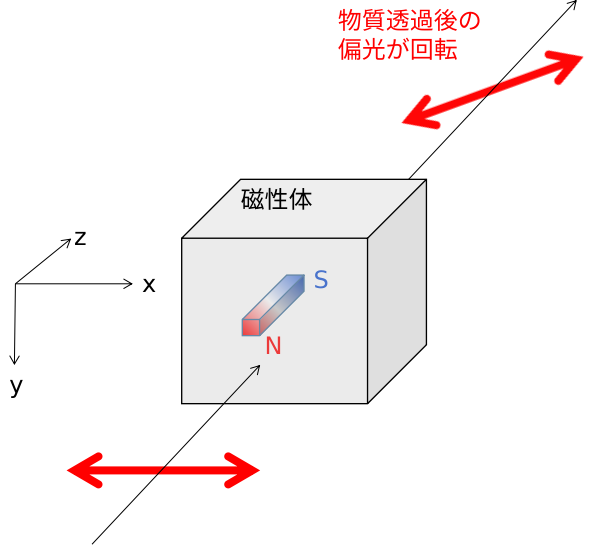
光の進行方向に平行な磁場が印加された磁性体中を光が進む場合、光の偏光が回転する現象は1845年にマイケル・ファラデーによって発見され、「ファラデー効果」と呼ばれます。磁性体とは、磁場を印加したときに磁石の性質を持つ物質のことであり、例えば磁石にくっついた鉄釘の先に別の鉄釘をくっつけることができるのは、鉄が磁性体だからです。
ファラデー効果の大きさの導出方法はThorlabsのサイトで解説されています。
対称性とマクスウェル方程式から導出可能
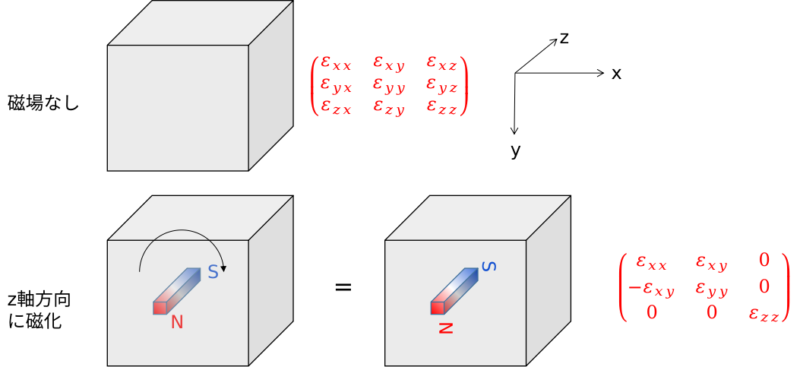
電池でx軸方向に電場Eをかけたら、電流がx軸方向に流れます。これはx軸方向に電荷Pが貯まると考えることができ、比例係数(誘電率)\(\varepsilon\)を用いて\(P=\varepsilon E\)と表せます。これをx,y,z全ての方向の組み合わせについて書いたのがテンソルと呼ばれる行列であり、以下の図(磁場なし)のようになります。例えば\(\varepsilon_{xy}\)はy軸方向に電場を印加したときにx軸方向に生じる電荷の比例係数です。磁場が無いときには電場に対してあらゆる方向に全部で9つの成分があります。
z軸方向に磁場を印加してz軸方向にN極・S極が生じた場合、z軸の周りにこの物質(磁性体)を90度回転させても元の状態と区別は付きません。この90度回転操作をC4とすると、
$$
\begin{pmatrix}
\varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz}\\
\varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz}\\
\varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz}
\end{pmatrix}=C_4
\begin{pmatrix}
\varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{xz}\\
\varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz}\\
\varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz}
\end{pmatrix}
$$
という関係が成り立ち、方程式を解くことでz軸方向に磁化した磁性体中の誘電率テンソルは
$$
\begin{pmatrix}
\varepsilon_{xx} & \varepsilon_{xy} &0\\
-\varepsilon_{xy} & \varepsilon_{yy} & 0\\
0& 0 & \varepsilon_{zz}
\end{pmatrix}
$$となる。ただし、こちらは対称性的に\(\varepsilon_{xy}\) は有限になりうるということを示すのみで、測定してみると\(\varepsilon_{xy}=0\)(もしくは測定感度以下)ということもあります。
以上は誘電率一般の場合の話であり、光が感じる誘電率も上記と同様の形式です。
光の伝搬においてはマクスウェル方程式も考慮する必要があります。マクスウェル方程式はコイルに電流を流すと磁場が生じる「電磁誘導の法則」などをまとめた4つの式です。
上記の誘電率テンソルとマクスウェル方程式を組み合わせることで、光がどのように伝搬するかは計算することが可能です。計算の過程は『光と磁気』(朝倉書店、佐藤勝昭著)3章をご参照ください。
偏光回転をPythonで検証
直線偏光がファラデー効果を生じる磁性体に入射すると、磁性体中では右回り円偏光・左回り円偏光として進みます。直線偏光は同じ電場の振幅・位相を持つ右回り円偏光と左回り円偏光を重ね合わせたものになります。右回り円偏光と左回り円偏光で物質透過後の位相が異なる場合、透過後の直線偏光の位相は入射偏光に対して回転します。
上記の現象をPythonで検証しました。
入射偏光を\(\boldsymbol{E}_0=\left(
\begin{array}{c}
E_{x} \\
E_{y} \\
E_{z}
\end{array}
\right)\)、\(i\)を虚数単位、\(\omega \)を角振動数(周波数に2\(\pi\)をかけたもの)、\(t\)を時間、光の進行方向を表すベクトル(波数ベクトル)を\(\boldsymbol{K}\) 、位置を\(\boldsymbol{r}\) とすると平面波は\(\boldsymbol{E}=\boldsymbol{E}_0exp(-i\omega t)\cdot exp(i\boldsymbol{K}\cdot \boldsymbol{r})\)と表すことができます。z軸方向に進むx軸方向の直線偏光は平面波の式において
\(\boldsymbol{E}_0=\left(
\begin{array}{c}
E_{x} \\
0\\
0
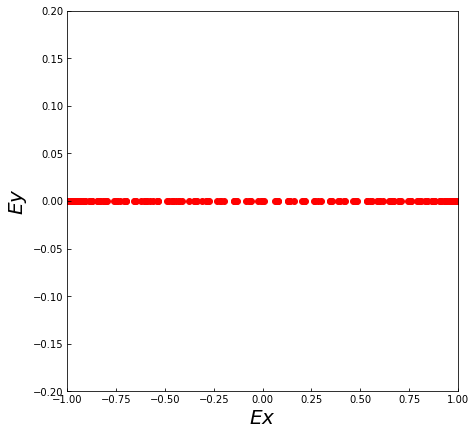
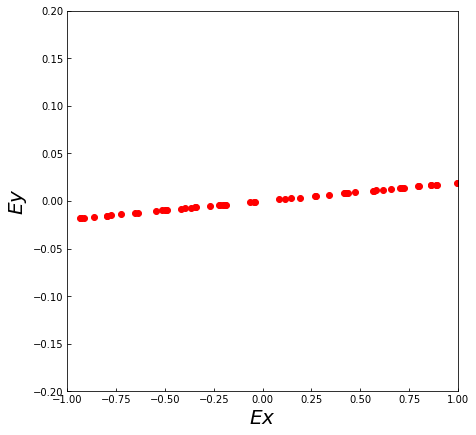
\end{array}\right)\)とすれば良いです。直線偏光であるかの検証の方法としては、ある位置\(\boldsymbol{r}\) で時間\(t\)を変化させたときに電場成分の軌跡(\(E_x,E_y\))が直線を描くかチェックすれば良いです。上記で設定した入射光の電場成分の軌跡をプロットすると、以下のように直線偏光になっていることがわかります。
#直線偏光
from sympy import *
from scipy import pi,sin,cos,tan,arcsin,linspace
import numpy as np
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
#変数設定
list_incident=[(w, 2*pi*5.6e+14), (c, 3e+8),(z,1e-3),(Ex,1),(Ey,0),(n,1)]#パラメータを変える場合はここを変更
x,y,z,Ex,Ey,Ez,w,t = symbols("x y z Ex Ey Ez w t")
r=Matrix([x, y, z])
E0 = Matrix([Ex, Ey, Ez])
K= Matrix([0, 0, w*n/c])#光が進む方向のベクトル(波数ベクトル)#w:角振動数、n:物質中の屈折率、c:真空中での光速
#直線偏光を設定
E_incident=E0*exp(-1j*w*t)*exp(1j*(K.T*r)[0,0])
E_incident=E_incident.subs(list_incident)
#print(E_incident)
#直線偏光を描画
t3_deg=linspace(0,180,181)#角度を0-180度の範囲で振る
#t3=t3_deg/180*pi
plt.figure(figsize=(7,7))
for t_ in t3:
plt.scatter(re(E_incident[0].subs(t,t_/180*pi)),re(E_incident[1].subs(t,t_/180*pi)),c="red")
plt.xlim(-1,1)
plt.ylim(-0.2,0.2)
xlabel(r"$Ex$",fontsize=20)
ylabel(r"$Ey$",fontsize=20)
plt.show()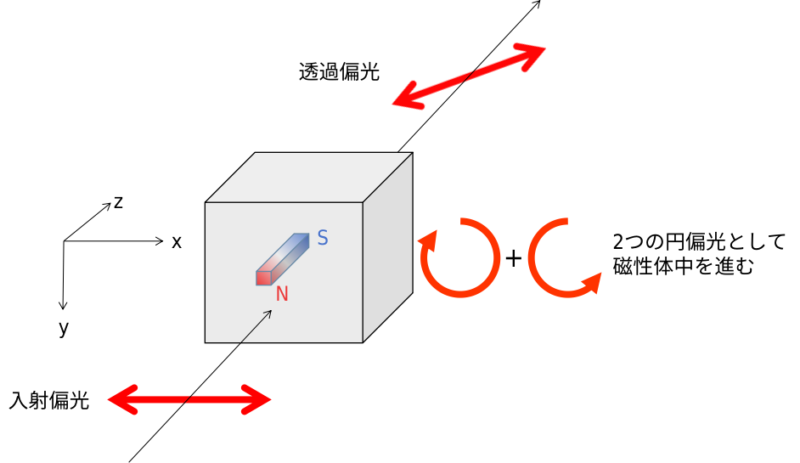
ファラデー効果を生じる磁性体中では直線偏光は右回り円偏光・左回り円偏光として進みます。誘電率テンソル\(\tilde{\varepsilon}\)の物質中を進む光の電場成分は、マクスウェル方程式から導かれる固有方程式を満たさなければなりません。固有方程式を解くことで、ファラデー効果を生じる磁性体中においては直線偏光は右回り円偏光と左回り円偏光に分離して進むことを導けます。(導出は『光と磁気』(朝倉書店、佐藤勝昭著)参照)
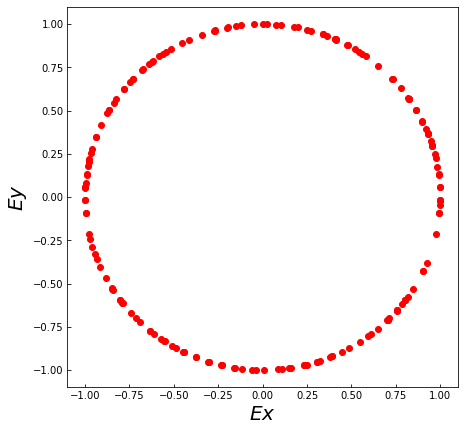
固有方程式から固有値・固有偏光(右回り円偏光と左回り円偏光)を求めました。固有ベクトルの1つをプロットすると、それが円偏光であることがわかります。
透過後の電場成分(右回り円偏光+左回り円偏光)を計算してみると、入射偏光に対して偏光の方向が傾いた直線偏光として出射することが確認できました。
ソースコードは以下になります。基本は教科書に沿って計算しています。list_allのパラメータの値を変えれば別の物質にも適用可能です。変数をsymbolsで設定することで変数のまま計算ができます。変数を用いて簡単に計算ができる例は「Pythonで変数を用いた固有値計算」でも紹介しています。
#z軸方向に磁化をもつ磁性体中の誘電率テンソル
e_xx,e_xy,e_yy,e_zz = symbols("e_xx e_xy e_yy e_zz ",real=True)
epsilon=Matrix([[e_xx, e_xy, 0],
[-e_xy, e_xx, 0],
[0, 0, e_zz]])
#入射偏光を定義 波数ベクトルK=N_hat*w/c
c,w = symbols("c w",real=True)
N = symbols("N")
N_hat=Matrix([0, 0, N])
x,y,z,t = symbols("x y z t",real=True)
Ex,Ey,Ez= symbols("Ex Ey Ez")
r=Matrix([x, y, z])
E0 = Matrix([Ex, Ey, Ez])
E=E0*exp(-1j*w*(t-(N_hat.T*r)[0,0]/c))
#マクスウェル方程式から導かれる、平面波が満たすべき式(固有方程式)
eq=(N**2)*E-(E.T*N_hat)[0,0]*N_hat-epsilon*E
#display(eq)
#固有値を導出
Coef=Matrix([[eq[0].coeff(Ex, 1),eq[0].coeff(Ey, 1)],[eq[1].coeff(Ex, 1),eq[1].coeff(Ey, 1)]])#Ex,Eyの項の係数(2×2行列)抽出
Coef=simplify((Coef)/(exp(-1j*w*(t-(N_hat.T*r)[0,0]/c))))#全ての項に共通の部分を除去。simplifyで式整理
display(Coef)
Det=Coef.det()
#print(Det)
s=solve(Det,N**2)#固有値の2乗の値を導出
display(s)
Ey1=solve((s[0]-e_xx)*Ex-e_xy*Ey,Ey)#固有値を代入して固有ベクトルのy成分を導出(Ey1,Ey2)
Ey2=solve((s[1]-e_xx)*Ex-e_xy*Ey,Ey)
print('Ey1:',solve((s[0]-e_xx)*Ex-e_xy*Ey,Ey))
print('Ey2:',solve((s[1]-e_xx)*Ex-e_xy*Ey,Ey))
#print(Ey_1)
N1,N2 = symbols("N1 N2")
E1=Matrix([Ex, Ey1[0], Ez])*exp(-1j*w*(t-N1/c*z))#固有ベクトルその1
E2=Matrix([Ex, Ey2[0], Ez])*exp(-1j*w*(t-N2/c*z))#固有ベクトルその2
#固有ベクトルの1つに着目→円偏光であることを確認
print("固有ベクトルの1つ:",E1)
#print(E2[1])
print("x成分:",simplify(re(E1[0].coeff(Ex, 1))))#変数の状態で、固有ベクトルの1つのx,y成分の係数を導出
print("y成分:",simplify(re(E1[1].coeff(Ex, 1))))
list_epsilon=[(e_xx, 16),(e_xy,0.3j)]
n1=sqrt(s[0]).subs(list_epsilon)#sが2つ解を持ち、固有値は±√|s|の計4つ。±√sの±それぞれでの2つの固有円偏光の結果は変わらないため、プラス側の2つを以下では考える。)
n2=sqrt(s[1]).subs(list_epsilon)
#パラメータの数値代入
list_all=[(w, 2*pi*5.6e+14), (c, 3e+8),(z,1e-3),(N1,n1),(N2,n2),(Ex,1)]
t3_deg=linspace(0,180,181)
t3=t3_deg/180*pi#入射角t1
#1つの固有ベクトルを描画→円偏光であることを確認
f0=re(E1[0].coeff(Ex, 1))#固有ベクトル1のx成分
f1=re(E1[1].coeff(Ex, 1))#固有ベクトル1のy成分
g0=f0.subs(list_all)#固有ベクトル1のx成分にパラメータ代入
g1=f1.subs(list_all)#固有ベクトル1のy成分にパラメータ代入
#print('f1:',f1)
#print('g1:',g1)
print(simplify(re(E1[0].coeff(Ex, 1))))
plt.figure(figsize=(7,7))
for t_ in t3:
plt.scatter(g0.subs(t,t_),g1.subs(t,t_),c="red")
#plt.xlim(-1,1)
#plt.ylim(-0.2,0.2)
xlabel(r"$Ex$",fontsize=20)
ylabel(r"$Ey$",fontsize=20)
plt.show()
#透過光(2つの固有ベクトルの和)を導出
Transmitted_light=simplify(E1+E2)
print("Transmitted light↓")
display(Transmitted_light)
#print(E1[0])
Transmitted_x=simplify(Transmitted_light[0].subs(list_all))#透過光のx成分にパラメータ代入
Transmitted_y=simplify(Transmitted_light[1].subs(list_all))#透過光のy成分にパラメータ代入
print('Transmitted_x:',Transmitted_x)
print('Transmitted_y:',Transmitted_y)
#透過光描画
plt.figure(figsize=(7,7))
for t_ in t3:
plt.scatter(re(Transmitted_x.subs(t,t_)),re(Transmitted_y.subs(t,t_)),c="red")
plt.xlim(-1,1)
plt.ylim(-0.2,0.2)
xlabel(r"$Ex$",fontsize=20)
ylabel(r"$Ey$",fontsize=20)
plt.show()Copyright © 2001-2020 Python Software Foundation; All Rights Reserved
Copyright © 2022 Released under the BSD License https://opensource.org/licenses/BSD-3-Clause


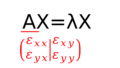

コメント